Hoog-dimensionale data ordenen met driehoekjes en velden
Supersnel driehoekjes tekenen en neurale netwerken lijken weinig met elkaar gemeen te hebben. Maar een slim inzicht van Nicola Pezzotti bracht de twee bij elkaar. Het visualiseren van verbanden in hoog-dimensionale data vergt niet langer tientallen minuten op een snelle computer, maar kan nu in real-time in een webbrowser. Ideaal voor het valideren van neurale netwerken. Biomedische onderzoekers van het LUMC maken er ook graag gebruik van.
“De wiskunde van algoritmes en schaalbaarheidsproblemen, dat is waar mijn hart sneller van gaat kloppen,” zegt Nicola Pezzotti, PhD-student binnen de Computer Graphics and Visualization groep. Hij vindt zichzelf bij uitstek een computerwetenschapper, maar de eerste tien minuten van ons interview vertelt hij juist vol enthousiasme over de praktische toepassingen van zijn werk. Zo heeft hij samen met het LUMC nieuwe cellen van het menselijk immuunsysteem gevonden, en hebben ze ook verschillende nieuwe stadia aangetoond in het differentiëren van stamcellen. “Onze data-visualisatie gaf het inzicht in het bestaan van die nieuwe cellen en tussenstadia, waarna het LUMC ze gericht ging zoeken en vond.” De belangrijkste toepassing van het werk van Nicola is echter bij het valideren van neurale netwerken. Om zijn onderzoek aan het t-SNE algoritme (t-distributed Stochastic Neighbor Embedding) te begrijpen is enige achtergrondkennis nodig.
Veel dimensies
Het werk van Nicola gaat niet zozeer over big data als wel over hoog-dimensionale data. “Dat betekent dat elk datapunt heel veel kenmerken heeft,” zegt Nicola. “In het LUMC kunnen ze van tientallen proteïnen bepalen in welke mate ze op het oppervlak van individuele cellen voorkomen. Elke cel is dan een datapunt met tientallen kenmerken.” Het weergeven van deze data zou dan ook een grafiek met

tientallen dimensies vereisen. Mensen kunnen daar niet mee overweg. Andere voorbeelden van hoog-dimensionale data zijn foto’s of handgeschreven cijfers. In gedigitaliseerde vorm zijn deze voor een computer te begrijpen en te ordenen. Maar met elke pixel een variabele (kleur, intensiteit, etc.) heeft elk datapunt zelfs duizenden dimensies.
De ruimte vervormen
Of het nu gaat om het herkennen van dieren op foto’s of het uitpluizen van welke genen een rol spelen bij een ziekte als borstkanker, neurale netwerken (‘deep neural networks’) zijn het vangnet voor het vinden van verbanden in deze data. “Een neuraal netwerk leert van een grote hoeveelheid trainingsdata, bijvoorbeeld foto’s van dieren,” legt Nicola uit. “Ze zoeken naar verbanden waarvan wij weten of vermoeden dat ze er zijn.” Het doel is, bijvoorbeeld, dat het netwerk onderscheid leert maken tussen een papegaai, een duif en een giraffe. Je vertelt bij elk trainingsplaatje wat het is en het netwerk zoekt zelf de kenmerken die daarbij blijken te horen. ‘Veel kleuren’ kan één van de kenmerken zijn voor ‘papegaai’. “Het neurale netwerk vervormt als het ware de hoog-dimensionale ruimte,” zegt Nicola. “Plaatjes die bij elkaar horen vormen dan clusters, zelfs als ze in die ruimte relatief ver uit elkaar liggen. Na de training zal het netwerk van een nieuw plaatje dat niet in de trainingsset voorkomt, maar dat ergens in die hoog-dimensionale ruimte ligt, meteen kunnen aangeven wat het is.”
Een olifant is geen duif
Maar zo eenvoudig is het niet. “De output van een neuraal netwerk is zelf ook weer hoog-dimensionaal,” legt Nicola uit. “Het is een rij getallen, een zogenaamde uitkomstvector, met daarin waarschijnlijkheden.” Het eerste getal geeft bijvoorbeeld de waarschijnlijkheid dat het nieuwe plaatje een papegaai is, het tweede getal de waarschijnlijkheid dat het een duif is, en zo verder. Al die waarschijnlijkheden tellen op tot het getal één, oftewel honderd procent. “Als het netwerk niet goed is ontworpen of als je het netwerk te weinig traint,” licht Nicola toe, “dan kan het geen goed onderscheid maken tussen de verschillende dieren.” Het netwerk zegt dan misschien dat een papegaai en een duif, of alles met vleugels, hetzelfde dier zijn. En als een duif het enige grijze dier in de trainingsset is, dan zullen een olifant en een nijlpaard er mogelijk bekaaid vanaf komen. Ontwikkelaars willen neurale netwerken ook met elkaar kunnen vergelijken. Welke is beter? “Een visuele weergave geeft het snelst inzicht in de kwaliteit van een neuraal netwerk,” legt Nicola uit, “en of er misschien meer of andere trainingsdata nodig is.” Een mens kan slechts drie dimensies overzien. Het weergeven van de (vervormde) hoog-dimensionale ruimte ‘in’ het netwerk is hiervoor dus geen optie. Gelukkig zijn er algoritmes die inzicht kunnen verschaffen in de verbanden in een hoog-dimensionale dataset, zoals de uitvoer van een neuraal netwerk. Met name het t-SNE algoritme, waar Nicola aan gewerkt heeft, is hier heel goed in.
Neurale netwerken en tSNE
Een getraind neuraal netwerk kan nieuwe data meteen classificeren. Het kan, bijvoorbeeld, van een enkele nieuwe foto aangeven dat het ‘een papegaai’ is. Het t-SNE algoritme visualiseert de verbanden die er zijn binnen een hoog-dimensionale dataset. De output van het algoritme is een grafische weergave van clusters van datapunten, zonder dat het aan kan geven of het cluster bestaat uit ‘vogels’ of foto’s van ‘een papegaai’.
Terug naar twee dimensies
Laurens van der Maaten, voormalig universitair hoofddocent aan de TU Delft en nu onderzoeker bij Facebook AI Research, publiceerde in 2008 over het t-SNE algoritme als verbetering op het dan al bestaande SNE algoritme. Beide algoritmes zijn erop gericht de samenhang in een hoog-dimensionale dataset weer te geven in een laag aantal dimensies, geschikt voor de mens. “Dit kan een driedimensionale weergave zijn,” zegt Nicola, “maar in mijn werk richt ik me op weergave in het tweedimensionale vlak (2D). Het is hierbij essentieel dat de laag-dimensionale weergave een goede, maar uiteraard niet perfecte, representatie is van de verbanden die bestaan tussen de hoog-dimensionale data.”
Nicola legt uit dat het t-SNE algoritme uit twee stappen bestaat. Stel, je hebt een dataset van honderdduizend uitkomstvectoren, het resultaat van nieuwe dierenplaatjes die door een reeds getraind neuraal netwerk zijn gecategoriseerd. Eerst berekent het algoritme de afstand tussen alle uitkomstvectoren in de hoog-dimensionale ruimte. Datapunten die op elkaar lijken, en waartussen een kleine afstand bestaat, vormen een hoog-dimensionaal cluster. Daarna zoekt het algoritme door middel van optimalisatie naar de 2D-weergave van alle datapunten die hier het best bij past. Datapunten die veel op elkaar lijken, moeten in de 2D-weergave dus ook dicht bij elkaar liggen, clusteren, en degenen die weinig gemeen hebben moeten juist ver(der) uit elkaar liggen.
Aantrekkende en afstotende krachten
Het al dan niet clusteren van datapunten in de 2D-weergave is letterlijk een krachtenspel. Het algoritme vertaalt de afstand tussen datapunten naar aantrekkende en afstotende krachten. Hoe meer twee datapunten op elkaar lijken, hoe groter de aantrekkende kracht. “Maar omdat alle datapunten altijd wel een klein beetje op elkaar lijken,“ legt Nicola uit, “is er ook een afstotende kracht nodig. Anders eindigen alle datapunten op een hoop.” Het oorspronkelijke SNE algoritme was traag omdat het beide krachten tussen àlle afzonderlijke datapunten berekende. “In dit geval schaalt het aantal berekeningen van afstanden en krachten kwadratisch met het aantal datapunten, en daarmee ook de rekentijd”, aldus Nicola. “En je hebt juist veel datapunten nodig om een gevoel te krijgen voor hoe goed een neuraal netwerk is in zijn taak.”
Het is deze kwadratische explosie van het aantal berekeningen dat van het t-SNE algoritme zo’n schaalbaarheidsprobleem maakt waar Nicola graag zijn tanden in zet. In de loop der jaren is het SNE algoritme al enkele malen verbeterd. De t-SNE implementatie van Laurens van der Maaten beperkte het berekenen van de aantrekkende krachten tot datapunten die dichtbij elkaar liggen. “De aantrekkende kracht is toch heel klein voor datapunten die weinig op elkaar lijken, die ver bij elkaar vandaan liggen, dus die kan je negeren,” aldus Nicola. Daarnaast verzon hij zelf dat de afstanden tussen de hoog-dimensionale datapunten met enige onnauwkeurigheid kunnen worden bepaald. “Dat maakt deze berekening veel sneller zonder dat het ten koste gaat van het eindresultaat.”
Met de blik van Einstein
Het recente en baanbrekende inzicht van Nicola gaat echter over het berekenen van de afstotende krachten. Dit was het als enige overgebleven tijdrovende element in het algoritme. Tijdens een stage bij Google in Zürich werkte hij zijn idee uit. Binnen het vakgebied van de visuele analyse is men lyrisch over zijn aanpak. Een fan twittert zelfs over ‘het onderzoek van een klerk uit Bern’, daarmee doelend op Einstein die zijn speciale relativiteitstheorie ontwikkelde terwijl hij als klerk werkte bij het octrooibureau in Bern. Nu gaan vergelijkingen met Einstein bijna altijd mank, maar het inzicht van Nicola vertoont wel degelijk overeenkomsten met dat van Einstein. “Het heersende paradigma bij de t-SNE optimalisatie is om het te benaderen vanuit het perspectief van interacties tussen alle datapunten onderling,” legt Nicola uit. “Meestal wil je zo’n paradigma niet veranderen. Ik besloot om de punt-naar-punt berekeningen voor de afstotende kracht te vervangen door het idee van een ‘veld’.”
In de aanpak van Nicola projecteert ieder datapunt in de 2D-weergave een afstotende kracht op een vierkant stukje ‘ruimte’ om zich heen, en creëert daarmee een klein veld. Datapunten in deze ruimte die zich dicht genoeg in de buurt bevinden, ondergaan door dat veld een kracht in het tweedimensionale vlak, en omgekeerd. In plaats van een voor een de invloed van alle datapunten op elkaar te bepalen, somt Nicola alle kleine veldjes op tot een globaal veld in de tweedimensionale ruimte. Soms versterken de velden van de afzonderlijke punten elkaar, en op andere posities zullen ze elkaar juist verzwakken of zelfs helemaal uitdoven. Vanuit dat globale veld berekent hij de afstotende kracht naar ieder datapunt afzonderlijk. Voor ieder datapunt hangen de richting en grootte van deze afstotende kracht dus alleen nog maar af van de positie van dat datapunt ten opzichte van dit globale veld. Bij elke stap in het optimalisatieproces worden het globale veld en de afstotende krachten opnieuw bepaald. Het uiteindelijke algoritme berekent drie velden: Voor de horizontale krachten, voor de verticale krachten en een normeringsveld zodat de optimalisatie goed verloopt. “Het lijkt extra werk, omdat ik de velden ook bereken waar helemaal geen datapunten zijn. Maar de velden kunnen een hele lage resolutie hebben en de aanpak is bovendien zeer geschikt voor implementatie op een grafische processor.” De vierkante veldjes om ieder datapunt bestaan uit twee driehoekjes met daarop een patroon (zie figuur). Dit is precies waar een grafische processor heel snel mee uit de voeten kan. Het resultaat is dat het algoritme een factor honderd sneller is geworden in vergelijking met reeds bestaande implementaties. Een onderzoeker kan het optimalisatieproces nu in real-time volgen, zelfs in een webbrowser, in plaats van tientallen minuten te moeten wachten op het eindresultaat. “Mijn implementatie kan veel grotere datasets aan. Daarnaast geeft real-time weergave de onderzoekers extra mogelijkheden. Ze kunnen het proces eerder stoppen om bijvoorbeeld het neurale netwerk extra te trainen, of juist inzoomen op een bepaald cluster voor extra detail.”
Exploderende complexiteit:
Het oorspronkelijke SNE algoritme berekent krachten tussen alle datapunten.
- Met drie datapunten zijn dat drie krachten, tussen de punten A-B, A-C en B-C.
- Met vier datapunten zijn dit zes krachten (A-B, A-C, A-D; B-C, B-D; C-D).
- Met tien datapunten zijn dit 45 krachten.
- Voor N datapunten zijn dit (N∙(N-1))/2 = (N2-N)/2 krachten. Het schaalt dus met N2.
- Voor 10.000 punten zijn dit bijna vijftig miljoen berekeningen!
Om de rekentijd acceptabel te houden zoeken computerwetenschappers naar oplossingen die schalen met N of ten hoogste met N∙log(N).
Het vervangen van krachten door een veld is precies wat Einstein deed. Hij verving de zwaartekracht - tussen planeten, sterren en andere objecten - door de gekromde ruimtetijd. In zijn theorie hangt de zwaartekracht op een object af van de kromming in de ruimte op de plek waar het object zich bevindt.
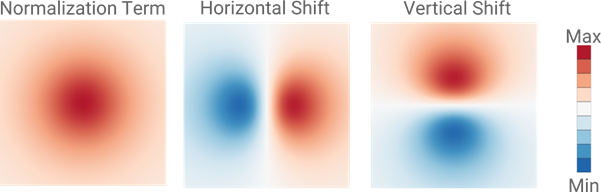
De drie velden rond een individueel datapunt, hier uitvergroot weergegeven. Het datapunt bevindt zich in het centrum van ieder van deze drie plaatjes. In de twee rechter plaatjes geeft een negatieve waarde (blauwe kleur) een afstotende kracht naar links of beneden weer.
Voor iedereen beschikbaar
Het algoritme van Nicola maakt nu onderdeel uit van ‘Tensorflow.js’, de open source software van Google voor onder andere het ontwerpen, trainen en analyseren van neurale netwerken. “Ik vind het belangrijk dat software open source is en door iedereen gebruikt kan worden. Dus niet alleen door universiteiten of bedrijven die een grote computer-infrastructuur kunnen aanschaffen en onderhouden. Mijn doel was dan ook om het algoritme zo snel te maken dat het op een enkele desktop-pc gebruikt kon worden.” De inzichten van Nicola zijn ook gepubliceerd in vakbladen. Maar hij wil meer. Het daadwerkelijk analyseren van hoog-dimensionale data blijft te ingewikkeld voor iemand die geen expert is. “Gelukkig bestaat onze vakgroep uit zeer goede en gedreven computerwetenschappers, met verschillende interesses.” Zijn collega Thomas Höllt werkt aan een softwareplatform, genaamd Cytosplore, dat de vertaalslag maakt tussen het algoritme en de biomedische onderzoekers van het LUMC. “Hij bouwt niet alleen een grafische interface met daarachter een stuk dataverwerking. Hij luistert precies naar wat zij nodig hebben om zelfstandig met hun onderzoeksdata aan de slag te kunnen.” De toepassingen van Nicola’s werk beperken zich zeker niet tot het medische vakgebied en neurale netwerken. Een student in de vakgroep heeft het algoritme al toegepast op de spelersstatistieken in baseball. Zelf deed hij er onderzoek mee naar filterbubbles bij het gebruik van sociale media. Nu nog een algoritme dat mijn elektriciteitsrekening begrijpelijk maakt.
Deze film geeft in real-time de optimalisatie weer van het t-SNE algoritme op de MNIST dataset. Deze dataset bestaat uit zestigduizend gedigitaliseerde handgeschreven cijfers, van 0 tot en met 9. Linksboven de 2D-weergave van deze hoog-dimensionale dataset, waarbij elk cijfer een specifieke kleur heeft. Linksonder en rechtsonder het globale veld voor de afstotende kracht, van alle datapunten bij elkaar opgeteld. Hieruit berekent het algoritme de horizontale en verticale afstotende krachten. Rechtsboven het normalisatieveld. Aan het begin van de simulatie voert het algoritme een truc uit en brengt het alle datapunten geforceerd naar elkaar toe. Hierdoor naderen op elkaar lijkende punten elkaar dicht genoeg zodat de aantrekkende krachten tot clustervorming leiden.
Tekst: Martijn Engelsman | Foto: Thierry Schut | Juli 2018
Klik hier om de Portraits-of-Science bijdrage van Nicola Pezzotti te lezen.